Building a Conceptual Understanding of Math With and Without Manipulatives

Written by: Shari Pyle

September 12, 2019

The Objective of Math Block 

According to many experts, including Wheatley & Reynolds (2010), mathematics involves much more than memorizing facts and completing math problems. Math has much more to do with understanding the connections between number  patterns and relationships. As NILD educational therapists our desire and objective should be to lead the student to a solid understanding of number meaning, number relationships, improved  visual imagery, and the use of effective strategic thinking. Educational therapists use Math Block to purposely lead the student to a conceptual understanding of mathematics by providing the student a set of meaningful activities that provides opportunity to construct number patterns and relationships.  This is done primarily through the use of mental math thinking, especially pulling upon visual imagery, number relationships, and strategic thinking. But occasionally the use of concrete representations can help the student see a deeper connection.  Physical manipulatives and visual representations provide concrete representations in which the student can develop the imagery for abstract mathematical thinking. There are many variations that can and should be used, and we will conclude this discussion with some examples.

Mediating a Conceptual Understanding of Math

Mediating a conceptual understanding of math begins with intentionally planning opportunities for your student to discover how numbers work with one another, including specific tasks that allow the student to identify patterns with numbers, make numerical comparisons, and group numbers into units. These crucial opportunities provide avenues for the student to make sense of the mathematical procedures and gain fluidity and flexibility with numbers. As the student begins to understand how numbers can be broken apart and put back together in a new way, he or she will learn to think conceptually about math.  A conceptual understanding of math isn’t possible  without a strong foundation of number sense  (Baroody & Rosu, 2006). According to Feifer (2017), number sense (more accurately symbolic number sense) “refers to the ability to ascribe meaning and value to numeric symbols” (p.44). This includes understanding what a number means; for example, knowing that the symbolic representation of the number 5 represents a group of five items. It also involves reasonable estimation skills, understanding basic mathematical operations, and the ability to make quick comparisons (more than, less than, etc.). Number sense grows into the ability to make sense of mathematical procedures, mathematical fluidity and flexibility, and eventually the ability to quantify the world. According to Shumway (2001), developing number sense gives mathematics greater meaning and solution flexibility, she says, “mathematics becomes more about reaching understandings than following rigid sets of rules" (p.8). Thinking fluidly and flexibly with numbers increases a student’s ability to apply smaller mathematical ideas to more difficult math problems.

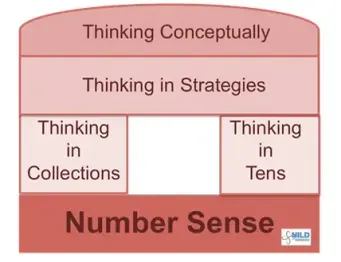
Though we have activities in Math Block that encourage rapid recall (partners of 10 and multiples factors), therapists need to be careful to avoid forming the habit of only asking students for acoustical sound bites that reflect rote memorization. Ask yourself, what is the greater meaning behind learning the partners of 10? Hopefully you answered that units of 10 become building blocks to understanding number relationships, and a basic tool used to formulate effective mathematical strategies. Internalizing basic math facts begins with the need to make sense and bring meaning to the relationship one math fact has to another. Memorizing math facts can increase efficiency and automaticity, but it does not build an understanding of mathematical concepts or numerical reasoning. Students need to understand number relationships in order to construct meaning of big ideas and math procedures.

Leading the student to think in collections and units of ten give the student competent tools for strategic thinking about number relationships. The student uses the number relationships to construct meaning of big ideas and develop a fuller understanding of math procedures. In other words, helping a student develop number sense, think in collections or groups of numbers and units of 10, along with self-generating strategies give the student the road map for improving mathematical reasoning and logical mathematical thinking. According to Piaget a student gains conceptual understanding when allowed to construct his knowledge by interacting with various ideas and comparing those ideas to what is already known (McLeod, 2018). In other words, a student who struggles with mathematical concepts needs to obtain a deeper understanding by exploring mathematical concepts and ideas, such as experiencing  structured play within Math Block.

During these specific and goal-oriented tasks the student should be  given opportunities to discover how numbers relate to one another, and how numbers can be grouped and broken apart. Manipulatives can aid this process as a concrete representation of the symbolic and naturally abstract meaning of math.

Math is Primarily Abstract

Mathematics requires multiple brain regions and structures to contribute and work harmoniously to process information efficiently (Feifer, 2017). Processing mathematically relies heavily upon nonverbal capabilities such as visual-spatial and fluid reasoning, but it also includes elements of language. Mathematics has a conglomerate of vocabulary words that can have unique meaning related only to numbers and mathematical operations. Using a wide variety of mathematical terms throughout Math Block is crucial for the fullest development of conceptual understanding.

Reviewing NILD goals and objectives for Math Block, we see that we are striving to give our student opportunities to form and retain visual image, improve auditory attention and listening skills, increase problem solving development, improve mathematical reasoning and logical thinking, develop mathematical vocabulary and concepts, internalize basic math facts, and improve language processing. Math Block activities should allow the student opportunity to utilize mathematical reasoning and other cognitive skills, while simultaneously providing situations that require  visual and verbal processing.

The use of manipulatives can aid the development of a conceptual understanding, but should only be used as needed. A struggling learner can grasp a concept or idea better when demonstrating his or her understanding with manipulatives or an illustration, so allow your students to use manipulatives to demonstrate connections between the abstract representation of mathematical symbols and concrete objects, and to prove solutions to math problems. The key element in using manipulatives is not to “show” the student what you mean, but rather to allow the student an opportunity to construct meaning for himself or herself.

Even though we know modeling is a form of scaffolding and it can be used to help a student reach the zone of proximal development, therapists need to avoid using manipulatives purely to demonstrate her or his numerical perspective. The therapist must deliberately guide the student’s thinking and allow the student to self-generate the connections. Therefore, careful attention needs to be given to how closely you mediate the student’s thinking.

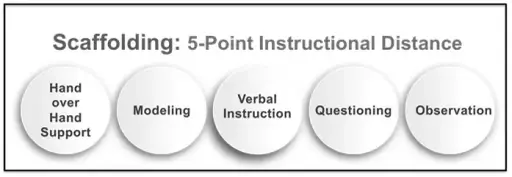
As a framework, consider the 5-points of distance with scaffolding: hand over hand support, modeling, verbal instruction, questioning, and observation. Obviously hand over hand is the closest support you can give your student and observation is most distant. In the NILD educational therapy setting we constantly move in and out each of these instructional distances according to the student’s needs; however, we rely heavily upon beginning with questioning and observation to best assess specific needs and capabilities. The same is true for Math Block. Therefore use manipulatives as an opportunity to observe your student’s understanding of the mathematical concept rather than modeling your understanding.

Balancing Abstract and Concrete Representations of Math

As a therapist you should be prepared to guide your student to move from the abstract to the concrete, and also from the concrete to the abstract. Once concepts are grasped, encourage the student to move from the self-generated concrete representation to the abstract symbolic representation, and visa versa.

For example, using partners of 10, we often have our student say the partners ... such as the following: “1-9, 2-8, 3-7, 4-6, 5-5, 6-4, 7-3, 8-2, 9-1.” Although we use this to increase rapid recall, it is the most abstract representation the student can use. Likewise, using the symbols 3 + 7 = 10 in a mathematical statement would be slightly more abstract than using additional language, such as “3 and 7 is 10”.

Mediate your student so that he or she can smoothly move from one form of expression to another. In addition, ask your student to  demonstrate or illustrate the relationship. There are many ways they can demonstrate their conceptual understanding from the most concrete, to an illustration, or usage of dot patterns.

Varying the modality and content can present a concept in a way that becomes more meaningful to your student. For example, after you ask a student for the multiples of 4 and the student says, “4, 8, 12, 16, 20, 24…48”, then ask the student to illustrate the multiples. This can be accomplished in many ways; one is represented in the picture below.

Begin by intentionally selecting math manipulatives that can be sorted into groups of four. Then observe how your student uses the manipulatives to demonstrate multiples of 4, mediating only as needed. Have your student explain the process he or she used, and then have him or her connect this knowledge to the appropriate symbolic representation.

Other options include using a mixture of concrete and abstract representations. In this example below, a picture of a balancing scale is used to compare the equal
value of coins; whereas on the right, coins are compared to the the symbolic representation of a monetary value.

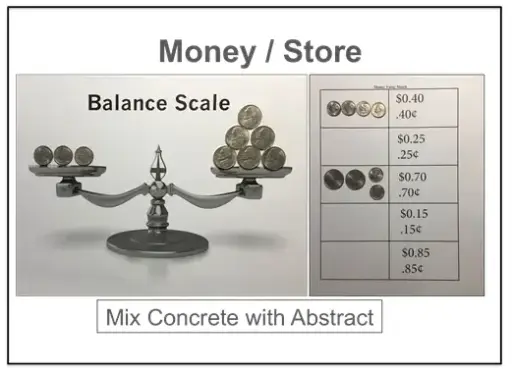
Remember the overarching goal for the Math Block technique is to increase the student’s ability to process mathematical thinking. Using it effectively begins with knowing your student’s current number sense knowledge, and knowing how the student needs to make mathematical connections.

Shari Pyle, MS, PCET, SL/DS

References

Feifer, S. (2017). The Neuropsychology of Mathematics. Middletown, MD. School Neuropsych Press, LLC, 25, 32-44.

McLeod, S. A. (2018). Jean Piaget’s Theory of Cognitive Development. Developmental Psychology. Retrieved from https://www.simplypsychology.org/piaget.html

McLeod, S. (2018). What is the Zone of Proximal Development. Developmental Psychology. Retrieved from https://www.simplypsychology.org/Zone-of-Proximal-Development.html#scaff

Shumway, J. F. (2001). Number Sense Routines. Portland, ME. Stenhouse Publishers, 8.

Wheatley, G. & Reynolds, A.. (2010). Coming to Know Number, 2nd Ed. Bethany Beach, DE. Mathematics Learning, 9-20, 27, 29.